Bitslog

Some time ago, I received an e-mail from my friend Timo Hanke. If you don’t know Timo, then you should, because he is, apart from a respected mathematician and Bitcoin enthusiast, an excellent person. The e-mail suggested that I looked into the nonce field to see if I could find out the endianess of Satoshi’s original mining machine. He was talking about the nonce in each block header, not the ExtraNonce I talked in my first post on Satoshi. My first thought was “nonces increase too quickly to leave any recognizable fingerprint”, but then I recalled that back in 2009 there were no GPUs and no ASICs and even if the nonce wrapped-around zero a couple of times, there would be a perceptible statistical imbalance towards zero in the most significant byte. So, armed with my own block-chain parser library, I prepared to begin a new fight against time and go back to the early days of Bitcoin. It took me half an hour to get my first surprise. One image worths a thousand words (or at least it stops a thousand false verbal arguments) so here is the image:

This image shows the least significant byte of the nonce, interpreted in a little endian machine, from the genesis block upto block 36288 (year 2010). This is neither an uniform distribution (which one would expect from a totally random byte) nor the decreasing exponential one would expect for the most significant byte of a big endian machine.

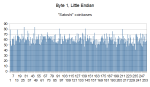
I’ll show you the most significant byte of the nonce, so you can compare.

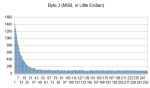This last graph clearly proves that almost all machines mining from 2009 to 2010 were little endian.

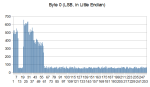
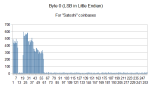
So the next thing I did is try to find the reason for such an awkward probability distribution in the LSB of the nonce. So I divided the graph into two: one for “Satoshi” coinbases and one for the remaining coinbases. To identify Satoshi coinbases I used a coarser method than the original: I just separated spent coinbases and unspent coinbases, which identifies Satoshi coins with good accuracy.

These are the corresponding graphs:

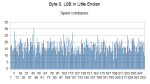
Now it was completely clear that the pattern belongs only to Satoshi mining machine. If you want to compare with a middle byte in the nonce of Satoshi nonces, this is how it looks:

That is how the byte 0 should have looked like if it were truly random.

So at this point I thought about four possible reasons for the imbalance:

A. My block chain parser is completely broken. Or my PC has been hacked and someone is playing a joke on me.

B. Satoshi was mining with a hardware very different from a PC. The imbalance was due to an optimization on the hardware, such as using gray codes for counting. In fact, the missing nonce values seems roughly compatible with a kind of decimal broken gray code. But this is too extravagant to be true. And nobody would use a decimal gray code instead of a binary gray code for a binary machine. But f this is true, then it has far reaching consequences: Satoshi foresaw the advantage of FPGA/ASIC much sooner than everybody else.

C. Satoshi discovered a flaw in SHA-2 so he didn’t need to go through all 32 bit nonces, just one fourth of them. Or he just solved some equations to find the nonce which gave only those restricted solutions. This is highly improbable.

D. Satoshi  left a message fingerprinted in the nonces. A Message for us to see in a distant future.

The number of nonces that fall into each byte value  or histogram (up to block 20000) begins with the following values:

0: 312
1: 286
2: 303
3: 276
4: 297
5: 301
6: 324
7: 276
8: 305
9: 247
10: 2 (the gap begins here)
11: 2
12: 2
13: 2
14: 3
15: 6
16: 5
17: 2
18: 5
19: 138
(high values from 20 to 58)

58: 201

59: 7 ( low values continue from here up to 255)

The selected set of bytes (0 to 9, 19 to 58) could have been selected to map a somewhat extended alphabet into this set. This must be explored further.

Another idea that crossed my mind is that the set itself has a kind of hidden message. It could refer to the date 18-10-1960 (taking the numbers between where the sequence changes with the exception of 1960 which should be 1958). 18-10-1960 is the date the article “Socialism, Inflation, and the Thrifty Householder” from Ludwig von Mises was published (see the article online). But this is something I made up in my head to justify the nonsense in the numbers, don’t you think? I am seeing order where there is no order at all, as in the film Pi?

We’re living in a LOST movie: each time it looks a mystery is solved, another one appears. I hope my friend Timo (the mathematician) now finds the hidden message and brings me some peace.

As always, I ask Bitcoin programmers to check my findings because errare humanum est.

Best regards, Sergio.

EDIT: It looks that Eyal0 got it right. His explanation of the probability distribution is the most convincing: it’s not a probability distribution at all! He suggested that Satoshi had access to 58 machines for mining, so to avoid checking the same nonce twice he gave each machine a different id, which was stamped in the LSB of the nonce. I think the reason the machines 10-18 are missing is because they belonged to the next Computer Lab in Satoshi’s faculty, but at the last time he was forgiven access to that Lab.

This explanation could be proved/disproved by checking the frequency of ExtraNonces going back in time. If too many computers are mining together (started at the same time) then one would expect one to be slightly faster than the other, so ExtraNonces are not synchronized. Then a machine with a lower ExtraNonce can solve a block just after a machine with a higher ExtraNonce, and time seams to go back.

EDIT2: Still another theory is that there were only 6 computers, each running a limited range of 10 LSB nonces. One of them broke, and was not used at the last moment. But I don’t buy it, since 58 is not divisible by 6.